Mecánica Cuántica | Física Computacional
03 – 2019
Se resuelve el Hamiltoniano de Bose-Hubbard en Wolfram Mathematica de manera exacta y con una aproximación de campo medio para analizar la transición de fase entre un Aislante de Mott y una fase superfluida.
Un ejemplo de un sistema físico con este comportamiento es un conjunto de ́átomos bosonicos fríos en una red óptica. De tal manera que los modos de la onda electromagnética actúan como pozos de potencial para los átomos.
Entonces, se puede pensar en un sistema de M sitios con un numero N finito de partículas que se distribuyen entre los M sitios, tal que a su vez las partículas pueden tener transiciones entre los sitios. Para el superfluido, la probabilidad de transición de una partícula a sus primeros vecinos es alta, de tal manera que hay muchas fluctuaciones de las particulas entre los sitios.
Diagonalización Exacta
Se construyó el hamiltoniano y se resolvió usando el comando Eigensystem. Primero se construye la base de estados. El número total de estados posibles está determinado por las combinaciones posibles del número de partículas por cada sitio, tal que el número de estados se incrementa rápidamente por (N+M-1)!/ [ N! (M-1)!]. Lo que exige más poder y memoria de computo.
Para reducir el número de operaciones, se usa un algoritmo lexicográfico, un algoritmo de etiquetado de estados.
Para comprender el algoritmo lexicográfico, uno puede observar las imágenes que representan los valores de dos matrices hamiltonianas. Ambas matrices son equivalentes. Ambas están describiendo el mismo sistema de M sitios y N partículas. Sin embargo, el cómo se va etiquetando los estados es distinto.
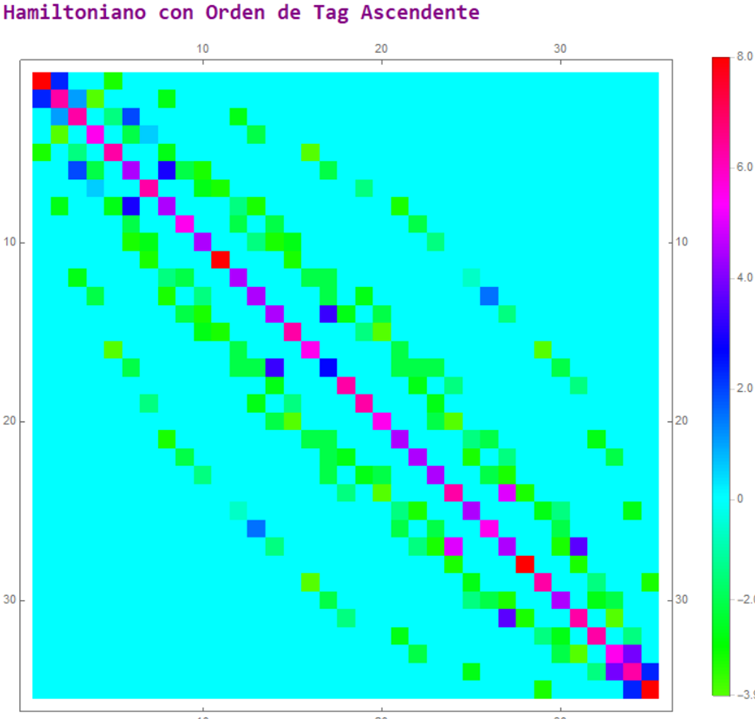
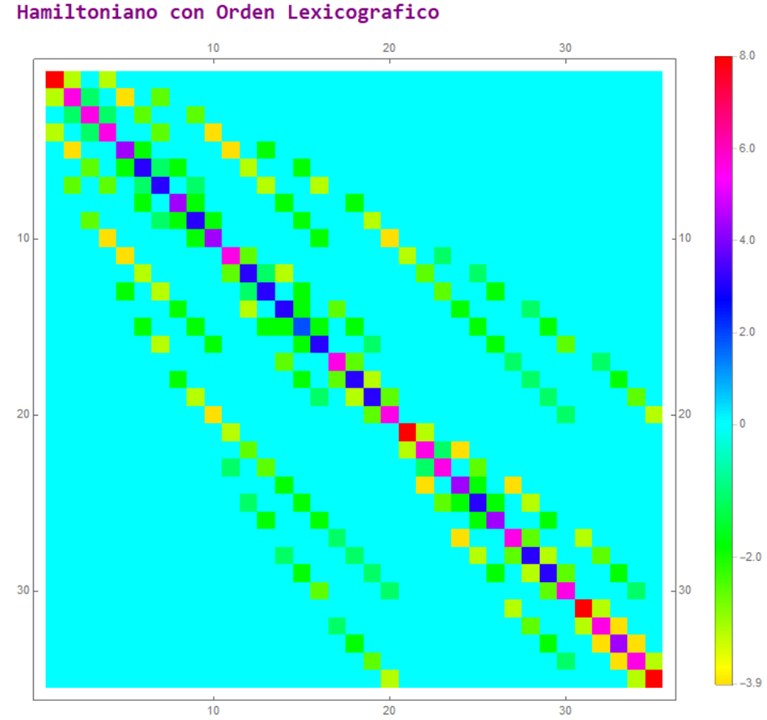
Por ejemplo, el etiquetado del 1er estado en el orden ascendente podría representar a las N partículas acomodadas consecutivamente en los sitios. Mientras que para el orden Lexicográfico, esa 1er estado sería otra configuración. Pero con el objetivo de simplificar los cálculos para la transición de estados, lo que reduce el costo computacional.
Al resolver este sistema 1D de forma exacta, se puede obtener un diagrama de la transición del sistema. La línea morada está indicando la región de transición entre dos fases. Lo que se apreciara mejor en la 2da parte del proyecto.
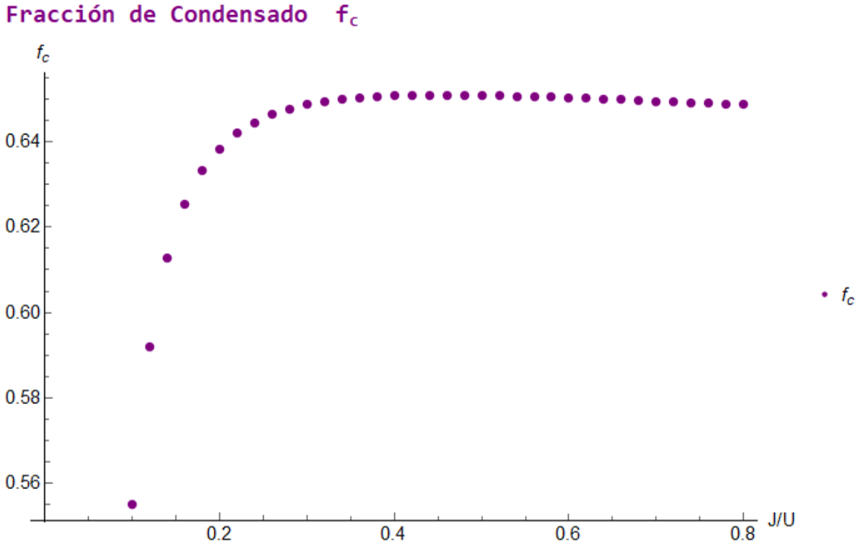
Aproximación de Campo Medio
La aproximación de Campo Medio plantea reducir un problema de un alto número de dimensiones en un modelo simplificado que promedia los grados de libertad. Esto se consigue remplazando las interacciones entre las N moléculas por interacciones efectivas modeladas como un campo de potencial.
Al resolver el sistema se puede graficar el diagrama de fase. Las zonas obscuras corresponden a la fase aislante de Mott, mientras las zonas claras corresponden a la fase superfluida. A la izquierda, el resultado de 3 zonas aislantes se obtuvo para N = 5 partículas. Y a la derecha, la zona con 2 aislantes corresponde a un sistema de N = 4 partículas.

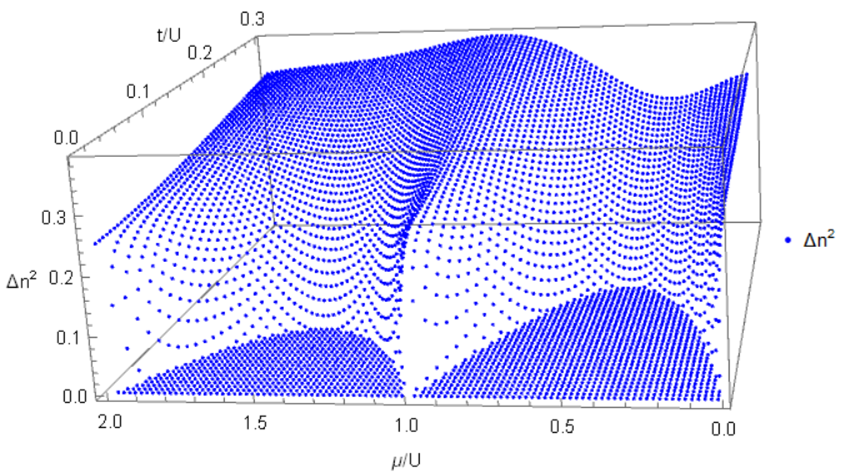
Variando el número de partículas, se puede concluir que las transiciones de fase pueden ocurrir a partir de un sistema de 3 sitios, tal que se van agregando zonas de transición conforme crece el número de sitios del sistema.
Consulta a detalle el Proyecto.
